Brady kim（阿金）

Brady kim（阿金）

몰라요. 그래서 배우고 있어요.

[기초 통계] 03 확률 분포와 정규분포

3 분 소요 

오류나 틀린 부분이 있을 경우 언제든지 댓글 혹은 메일로 남겨주세요 😄

통계 기초와 적용 - 02 중심화 경향,분산도, 표준화

표본 공간(Sample space)

  • 통계적 실험이나 조사에서 모든 가능한 실현 결과들의 집합

확률 변수(Random Variable)

  • 우리는 동전(Fair coin)을 2개를 동시에 던져서 얻는 결과가 앞인지 뒤인지 알고 싶다고 하자. 그렇다면, 우리는 다음과 같은 Variable을 관측할 수 있을 것이다.

img

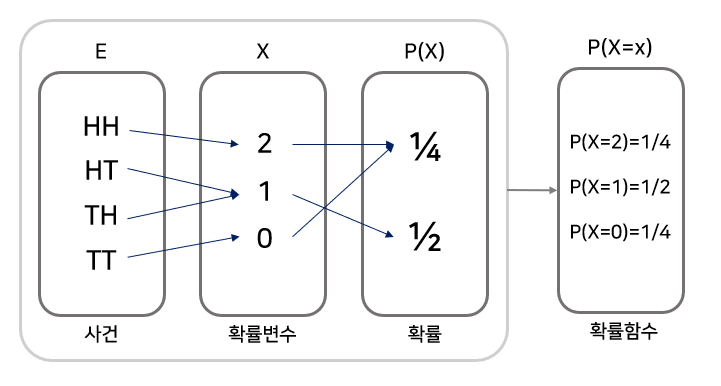
출처: https://dlearner.tistory.com/32

  • {앞Head,앞},{앞,뒤Tail},{뒤,앞},{뒤,뒤}와 같은 Variable을 각각의 ‘앞면이 나오는 개수’에 대해서 실수값에 대응시켜보자. 그렇다면 앞이 2번 나온 경우 X=2, HT,TH는 1, TT는 0일 것이다.
  • 이렇게 구해진 확률변수의 값을 확률로 나타낸다면,
    • 확률변수가 2인 경우는 전체 경우의 수의 1/4
    • 확률변수가 1인 경우는 전체 경우의 수의 2/4
    • 확률변수가 0인 경우는 전체 경우의 수의 1/4를 차지함
  • 즉, 확률 변수는 어떤 실험에서 나타날 수 있는 확률적 결과를 수치로 표현한 값이라고 할 수 있다.

확률 변수의 종류

  • 이산 확률변수(discrete random variable)

    동전 던지기, 주사위 던지기와 같이 확률 실험에서 나타날 수 있는 결과를 셀수 있는 사건의 경우

    위의 동전 던지기 예시에서, 앞이 나올 확률변수 X가 취할 수 있는 값 {2,1,0}을 셀 수 있음

  • 연속 확률변수(continuous random variable)

    연속적인 범위의 값을 지니는 확률변수임. 예를 들어, 동전이 앞면이 나오는 수는 위의 예시처럼 셀 수 있지만, 통계학을 공부한 시간은 셀 수 없다.X=1초

    X=1.0001초,X=1.00000001초 등 특정할 수 없기 때문이다. 따라서 연속 확률변수라면, 어떤 하나의 지점이 발생할 확률이 0에 가깝다고 하는 이유가 이 때문이다.

    따라서 연속 확률 변수는 특정 값이 아니라, 구간을 통해 확률을 설명해야 함.

확률 질량 함수

  • 이산 확률변수의 확률분포를 나타내는 함수로, 이산확률변수 X가 취할 수 있는 값 x1,x2,x3..에 대하여, 그에 대한 확률 P(X=x1),P(X=x2)를 대응시켜주는 함수임

확률 밀도 함수

  • 연속 확률 변수는 위에서 말한것 처럼 범위(ex. 통계공부 1시간부터 2시간 까지)를 확률 변수로 표현해야 하기 때문에 범위의 시작점을 가장 작은 숫자로 고정하여 하나의 확률 변수로 표현함

  • X=1 -> 통계 공부 0시간부터 1시간 -> 확률 1/24

  • X=2 -> 통계 공부 0시간부터 2시간 -> 확률 2/24

  • 이것을 표현한 함수를 누적 확률 밀도 함수라고 하는데, 일반적으로 CDF 또는 F(x)라고 쓴다.

    확률밀도함수의 색과 같은 색

정규분포의 CDF

  • 이러한 CDF는 어떠한 확률 변수 x의 값이 더 자주 나오는지에 대한 정보를 주기 어렵다. 따라서 이를 미분하여 나온 도함수를 이용하고 이를 확률밀도함수라고 함.

    • 어렵다. 간단하게, 일정한 범위에 있는 모든 실수의 값을 취할 수 있는 확률변수를 연속확률변수라고 하고, 이러한 확률변수가 이루는 분포를 연속확률분포라고 하자.

    • 그리고, P(a <= x <= b)의 확률값을 구하기 위해서는 확률밀도함수 f(x)와 X축의 두 실수 a와 b 사이의 넓이로 확률을 계산할 수 있다고 알고 있자.

      image

정규분포의 정의

확률분포 X가 다음의 확률밀도함수 f(x)를 가질 때, 확률변수 X는 평균이 μ 분산이 σ^2인 정규분포를 따른다.

image

  • 그럼 우리가 관측하고자 하는 사건이 이 정규분포를 따르는 사건이라면, 그 사건이 발생하는 확률을 우리는 계산할 수 있게 된다. 왜냐하면, 그래프의 넓이를 통해 확률값을 계산할 수 있다고 했으니 !

  • 일상에서 Heights of people, Blood pressure 등의 변수는 정규분포와 유사한 형태를 가진다고 함

    image

  • 또 정규분포는 앞에서 배운 Mean = Median = mode가 모두 같은 데이터의 분포를 가지고 있음

정규분포의 특징

  • 정규분포는 평균을 중심으로 대칭함.
  • 정규분포의 모습은 평균과 표준편차에 의해 결정됨
    • 표준편차가 크면 클 수록 옆으로 퍼진 형태가 됨
  • 정규분포를 나타내는 곡선의 약 68.2%는 평균을 중심으로 +-1 Standard deviation 의 영역에 있음
  • 정규분포를 나타내는 곡선의 약 95.4%는 평균을 중심으로 +-2 Standard deviation 의 영역에 있음

표준 정규분포

  • 표준 정규분포는 정규분포의 값들을 Z-score화 한것임

    image

  • 02 에서 설명한것과 같이, 여기서 분자는 평균이 0이 되도록 수평이동을 시키는 역할을 하며, 분포의 표준편차가 1이 되도록 Scaling 해주는 역할이다.

image

  • 표준정규분포표

    • 02에서 Z-score는 평균 0으로 부터 몇 표준편차 떨어져 있는지 보여주는 수치라고 하였다.

    • 부지런한 수학자와 통계학자들은 이 Z-score에 따라서, 표준정규분포에서 얼마의 확률값을 가지는지 계산하였고, 그 표가 표준정규분포표이다.

    image

    • Z=0.62는 0에서부터 0.62 표준편차 떨어져 있다고 하였다. 그리고 P(0 <=x <= 0.62)는 23.24%라고 나온다. 아래 표를 보자. 큰 Z 아래에 있는 0.0, 0.1, 0.2는 10^-1의 자리수, Z 왼쪽에 있는 수들은 10^-2의 자리수임.

      표에서도 0.2324가 나오는 것을 확인할 수 있음.

      image

      출처:https://www.mathsisfun.com/data/standard-normal-distribution-table.html

적용

  • 강아지의 길이가 정규분포를 따르고, 평균이 65(인치), 표준펀차가 3.5(인치)라고 하자.

  • 강아지 1명을 무작위로 뽑았을 때, 해당 강아지의 길이가 62.5인치에서 68.5인치사이에 있을 확률은?

    • 연속 확률 변수를 가지는 확률 밀도 함수는 그래프의 넓이를 통해서 확률을 계산할 수 있다고 하였다. 그리고 우리는 이 그래프가 정규분포를 따르는 것을 알고 있다. 그렇다면 그 정규분포(62.5,68.5) 사이의 넓이를 구하면 우리가 원하는 확률을 구할 수 있는 것임.

    • 그런데, 문제가 있다. 여기서 평균이 65이고, 표준편차가 3.5인 정규분포의 넓이를 쉽게 구할 수 없음. 따라서 이것을 표준화하여, 우리가 알고 있는 표준정규분포로 바꾸고, 누군가가 구해놓은 표를 통해 확률을 구할 수 있을 것임.

    • P(62.5<X<68.5)

      =0에서 68.5일 확률은? 평균 65에서 1Standard deviation 떨어짐. 이것을 표준정규분포로 생각해보면, Z-score가 1이고, 표에서 1.0을 확인해보면 0.3413

      =0에서 62.5일 확률은? 평균 65에서 -1Standard deviation 떨어짐. 이것을 표준정규분표로 생각해보면, Z-score가 -1이고 표에서 1.0을 확인해보면 0.3413

      따라서 P(62.5<X<68.5) = 0.6826

참고